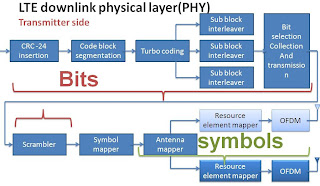
3.3 Cyclic redundancy check (CRC)
insertion:
In
the first step of the transport-channel processing is a 24-bit CRC, it is
calculated for and appended to each transport block. The CRC allows for
receiver side detection of errors in the decoded transport block. The
corresponding error indication is then, for example, used by the downlink
hybrid-ARQ protocol as a trigger for requesting retransmissions.
CRC is an error detection algorithms used
in modern communication and computer applications. In such a technique a block
of data is divided on a certain devisor. The remainder of the division is then
attached to the block of data and sent over the channel.
At
the decoder, the received data are divided on the same devisor and the
remainder is checked. If the remainder is equal zero so no syndrome appeared
and no error detected else the received data was not totally corrected. One of
the methods used in the CRC implementation, the module-2 binary division which
is illustrated by figure (3.3)
3.3.1 Forward error correction (FEC):
The sender adds (carefully selected)
redundant data to its messages, also known as an
error-correcting code. This allows the receiver to detect and correct errors
without the need to ask the sender for additional data.
The advantages of forward error
correction are that a back-channel is not required
and retransmission of data can often be avoided (at the cost of higher
bandwidth requirements, on average). FEC is therefore applied in situations
where retransmissions are relatively costly or impossible.
The two main categories of FEC codes
are block codes and convolutional
codes.
Block codes work on fixed-size blocks (packets) of bits or symbols of
predetermined size. Practical block codes can generally be decoded in polynomial time to their block length.
Convolutional codes work on bit or
symbol streams of arbitrary length. They are most often decoded with the Viterbi algorithm, though other
algorithms are sometimes used. Viterbi decoding allows asymptotically optimal
decoding efficiency with increasing constraint length of the convolutional
code, but at the The sender adds (carefully selected) redundant data to its messages, also known as an
error-correcting code.
This allows the receiver to detect
and correct errors without the need to ask the sender for additional data. The
advantages of forward error correction are that a back-channel is not required
and retransmission of data can often be avoided (at the cost of higher
bandwidth requirements, on average).
3.3.2
Convolutional encoder :
The encoder of a binary convolutional code
with rate 1/n,(ode rate is the number of parallel input/number of parallel
output) measured in bits per symbol, may be as a finite-state machine that
consists of an M-stage shift register with prescribed connections to n modulo-2
adders, and a multiplexer that serializes the outputs of the adders.
The
constraint length of a convolutional code, expressed in terms of message bits,
is defined as the number of shifts over which a single message bit can
influence the encoder output.
In an
encoder with an M-stage shift register, the memory of the encoder equals M
message bits, and K = M + 1 shifts are required for a message bit to enter the
shift register and finally come out. Hence, the constraint length of the
encoder is K. Figure 41 shows a convolutional encoder with n = 2 and K = 4.
Hence, the code rate f this encoder is 1/2.
Figure 3.4 -- convolutional encoder
---
By revising the
encoding algorithm in the slides you can find that, flushing zeros are add at
the start of the encoding to initialize the registers. Tail bits are added at
the end to restore the initial state. All these additional bits are used in the
decoding step which will be discussed later.
Equivalently,
we may characterize each path in terms of a generator polynomial, defined as
the unit-delay transform of the impulse response. For our encoder example the
impulse response of the first path can be represented by the bits “111” and
hence the generator polynomial will be 1+D+D2. Similarly the impulse response
of both the second polynomial and the input message will be 1+D2 and 1+D2+D4
consequently.
As fourier transform convolution in
the time domain will be converted into multiplication in the D domain. Hence
the first path output will be (1+D+D2)(1+D2+D4)=(1+D+D3+D5 D6)=”1101011”.
And the second path output will be
(1+D2)(1+D2+D4)=(1+ D6)=”100001”. The two paths outputs are then combined and
transmitted together as “11 01 00 01 00 01 11”.
Each decoder is having a previous
estimation to what the encoder generates at each case of inputs and in each
paths configuration.
For our encoder as it has three
stages so it has two state bits a one input bit.
Now we will put a full visualization
to all the present and next states with the estimated output at each case of
the input at figure (3.5)
Figure 3.5
We can represent this estimation in terms
of the state diagram, the tree diagram and the trellis digram. They are all
shown in figure (3.6)
Figure 3.6 ---
the tree diagram and the trellis digram
3.3.3 Veterbi
decoder :
The equivalence between maximum
likelihood decoding and minimum distance decoding for a binary symmetric
channel implies that we may decode a convolutional code by choosing a path in
the code tree whose coded sequence differs from the received sequence in the
fewest number of places. Since a code tree is equivalent to a trellis, we may
equally limit our choice to the possible paths in the trellis representation of
the code.
For
example we will assume the received data and the pre described trellis as shown
in figure (3.7). The figure contains only two states for more simplification in
the discussion.
Figure 3.7
We check each
channel output with each stage. Then, we are counting the error bits and is
added it to the previous path error. For a certain node, if two paths gave two
different errors the bigger one is discarded. The best path is then chosen
which have the minimum error.